Установите соответствие между графиками функций и характеристиками этих функций на отрезке [-1; 1].
[b]ХАРАКТЕРИСТИКИ
1) функция возрастает на отрезке [-1; 1]
2) функция убывает на отрезке [-1; 1]
3) функция имеет точку минимума на отрезке [-1; 1]
4) функция имеет точку максимума на отрезке [-1; 1]
На диаграмме показано количество запросов аббревиатуры ЕГЭ, сделанных на поисковом сайте Google во все месяцы с сентября 2015 года по август 2016 года. По горизонтали указываются месяца и год, по вертикали - количество запросов за данный месяц.
Пользуясь диаграммой, установите связь между промежутками времени и характером изменения количества запросов.
[b]ПРОМЕЖУТКИ ВРЕМЕНИ
А) Осень
Б) Зима
В) Весна
Г) Лето
[b]ХАРАКТЕР ИЗМЕНЕНИЯ КОЛИЧЕСТВА ЗАПРОСОВ
1) Резкий спад количества запросов
2) Количество запросов практически не менялось
3) Количество запросов плавно снижалось
4) Количество запросов плавно росло
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

На графике изображена зависимость частоты пульса гимнаста от времени в течение и после его выступления в вольных упражнениях.
На горизонтальной оси отмечено время(в минутах), прошедшее с начала выступления гимнаста, на вертикальной оси - частота пульса(в ударах в минуту).
Пользуясь графиком, поставьте в соответствие каждому периоду времени характеристику пульса гимнаста на этом периоде.

В таблице указаны доходы и расходы фирмы за 5 месяцев.
Пользуясь таблицей, поставьте в соответствие каждому из указанных периодов времени характеристику доходов и расходов.
В таблице под каждой буквой укажите соответствующий номер.

На рисунке точками показана среднесуточная температура воздуха в Москве в январе 2011 года. По горизонтали указываются числа месяца, по вертикали - температура в градусах Цельсия. Для наглядности точки соединены линией.
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику изменения температуры.

На графике изображена зависимость скорости движения легкового автомобиля от времени. На вертикальной оси отмечена скорость легкового автомобиля в км/ч, на горизонтальной - время в секундах, прошедшее с начала движения автомобиля.
Пользуясь графиком, поставьте в соответствие каждому периоду времени характеристику движения автомобиля на этом интервале.
ПЕРИОДЫ ВРЕМЕНИ
А) 0-30 с
Б) 60-60 с
В) 60-90 с
Г) 90-120 с
ХАРАКТЕРИСТИКИ
1) скорость автомобиля достигла максимума за всё время движения автомобиля
2) скорость автомобиля не уменьшалась и не превышала 40 км/ч
3) автомобиль сделал остановку на 15 секунд
4) скорость автомобиля не увеличивалась на всём интервале

A
B
C
D
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
1) -4
2) 3
3) 2/3
4) -1/2
В таблице под каждой буквой укажите соответствующий номер.

На графике изображена зависимость температуры от времени в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя; на вертикальной оси - температура двигателя в градусах Цельсия.
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.
ИНТЕРВАЛЫ ВРЕМЕНИ
A) 0-1 мин.
Б) 1-3 мин.
B) 3-6 мин.
Г) 8-10 мин.
ХАРАКТЕРИСТИКИ
1) самый медленный рост температуры
2) температура падала
3) температура находилась в пределах от 40 °С до 80 °С
4) температура не превышала 30 °С.

На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.

На графике изображена зависимость скорости погружения батискафа от времени. На вертикальной оси отмечена скорость в м/с, на горизонтальной - время в секундах, прошедшее с начала погружения.
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику погружения батискафа на этом интервале.
ИНТЕРВАЛЫ ВРЕМЕНИ
А) 60-150c
Б) 150-180c
В) 180-240c
Г) 240-300 c
ХАРАКТЕРИСТИКИ
1) Батискаф 45 секунд погружался с постоянной скоростью.
2) Скорость погружения уменьшалась, а затем произошла остановка на полминуты.
3) Скорость погружения достигла максимума за все время.
4) Скорость погружения не увеличивалась на всем интервале, но батискаф не останавливался.
В таблице под каждой буквой укажите соответствующий номер.

На рисунке изображён график функции у = f(x) и отмечены точки А, В. С и D на оси Ох. Пользуясь графиком, поставьте в соответствие каждой точке характеристики функции и её производной.
А) А
Б) В
В) С
Г) D
ХАРАКТЕРИСТИКИ ФУНКЦИИ И ПРОИЗВОДНОЙ
1) значение функции в точке отрицательно и значение производной функции в точке отрицательно
2) значение функции в точке положительно и значение производной функции в точке положительно
3) значение функции в точке отрицательно, а значение производной функции в точке положительно
4) значение функции в точке положительно, а значение производной функции в точке равно нулю

На рисунке изображён график функции y=f(х). Точки a, b, c, d и e
задают на оси Ох интервалы. Пользуясь графиком, поставьте в соответствие каждому интервалу характеристику функции или её производной.

На рисунке изображён график функции y=f(x). Точки a, b, c, d и e
задают на оси Ox интервалы. Пользуясь графиком, поставьте в соответствие каждому интервалу характеристику функции или её производной.

На диаграмме показаны объёмы месячных продаж холодильников в магазине бытовой техники в течение года. По горизонтали указываются месяцы, по вертикали - количество проданных холодильников.
Пользуясь диаграммой, поставьте в соответствие каждому из указанных периодов времени характеристику продаж данного товара.
А) январь-март
Б) апрель-июнь
В) июль-сентябрь
Г) октябрь-декабрь
ХАРАКТЕРИСТИКА ПРОДАЖ
1) наибольший рост объёма продаж
2) наименьший рост объёма продаж
3) достиг минимума за всё время
4) достиг максимума за всё время

На рисунке точками показано атмосферное давление в городе N на протяжении трёх суток с 4 по 6 апреля 2013 года. В течение суток давление измеряется 4 раза: в 0:00, в 6:00, в 12:00 и в 18:00. По горизонтали указываются время суток и дата, по вертикали - давление в миллиметрах ртутного столба. Для наглядности точки соединены линиями.

На рисунке точками показаны объёмы месячных продаж обогревателей в магазине бытовой техники. По горизонтали указываются месяцы, по вертикали - количество проданных обогревателей. Для наглядности точки соединены линией.

На диаграмме изображена цена акций компании в период с 1 по 14 сентября 2013 г. По горизонтали указываются числа месяца, по вертикали - цена акции в рублях.
Пользуясь диаграммой, поставьте в соответствие каждому из ука¬занных периодов времени характеристику цены акций.
А) 1-3 сентября 1)самое быстрое падение цены цена
Б) 4-6 сентября 2)росла в течение всего периода
В) 7-9 сентября 3)самое медленное падение цены
Г) 9-11 сентября 4)цена сначала увеличивалась, а потом стала уменьшаться

На графике изображена зависимость скорости движения рейсового автобуса от времени. На вертикальной оси отмечена скорость ав¬тобуса в км/ч, на горизонтальной - время в минутах, прошедшее с начала движения автобус
ИНТЕРВАЛЫ ХАРАКТЕРИСТИКИ
ВРЕМЕНИ ДВИЖЕНИЯ
А) 4-8 мин 1) была остановка длительностью 2 мин
Б) 8-12 мин 2) скорость не меньше 20 км/ч на всём интервале
В) 12-16 мин 3) скорость не больше 60 км/ч
Г) 18-22 мин 4) была остановка длительностью 1 мин

На диаграмме изображена цена акций компании в период с 1 по 14 сентября 2013 г. По горизонтали указываются числа месяца, по вертикали - цена акции в рублях.Пользуясь диаграммой, поставьте в соответствие каждому из указанных интервалов времени характеристику цены акций.

На рисунке точками показано атмосферное давление в городе N на протяжении трёх суток с 4 по 6 апреля 2013 года. В течение суток давление измеряется 4 раза: в 0:00,в 6:00, в 12:00, и в 18:00. По горизонтали указывается время суток и дата, по вертикали – давление в миллиметрах ртутного столба. Для наглядности точки соединены линиями. Пользуясь рисунком, поставьте в соответствие каждому из ука¬занных периодов времени характеристику атмосферного давления в городе N в течение этого периода.
Главная
Как подготовиться к решению заданий ЕГЭ № 14 по стереометрии | 1С:Репетитор
Как показывают результаты профильного экзамена по математике, задачи по геометрии - в числе самых сложных для выпускников. Тем не менее, решить их, хотя бы частично, а значит заработать дополнительные баллы к общему результату возможно. Для этого необходимо, конечно, знать достаточно много о «поведении» геометрических фигур и уметь применять эти знания для решения задач. Здесь мы постараемся дать некоторые рекомендации, как подготовиться к решению задачи по стереометрии.
Что нужно знать о задаче по стереометрии № 14 варианта КИМ ЕГЭ
Эта задача обычно состоит из двух частей:
За решение данной задачи на экзамене по математике в 2018 году можно получить максимум два первичных балла . Допускается решить только «доказательную» или только «вычислительную» часть задачи и заработать в этом случае один первичный балл.
Многие школьники на экзамене даже не приступают к решению задачи №14, хотя она значительно проще, например, задачи № 16 - по планиметрии.
В задачу № 14 традиционно включается лишь несколько вопросов из всех возможных для стереометрических задач:
В соответствии с этими вопросами строится и подготовка к решению задачи .
Сначала, разумеется, нужно выучить все необходимые аксиомы и теоремы , которые понадобятся для доказательной части задачи. Помимо того, что знание аксиом и теорем поможет вам на экзамене непосредственно при решении задачи, их повторение позволит систематизировать и обобщить ваши знания по стереометрии вообще, то есть создать из этих знаний некую целостную картину.
Итак, что же нужно выучить?
После того как вы повторили теорию, можно приступать к рассмотрению методов решения задач. В курсе «1C:Репетитор» представлены : видеолекции с теорией, тренажеры с пошаговым решением задач, тесты для самопроверки, интерактивные модели, позволяющие ученикам 10-х и 11-х классов наглядно рассмотреть методы решения задач по стереометрии, в том числе на примерах задач ЕГЭ 2017 года.
Мы рекомендуем решать задачи в такой последовательности:- Углы в пространстве (между скрещивающимися прямыми, между прямой и плоскостью, между плоскостями);
- Расстояния в пространстве (между двумя точками, между точкой и прямой, между точкой и плоскостью, между скрещивающимися прямыми);
- Решение многогранников, то есть нахождение углов между ребрами и гранями, расстояний между ребрами, площадей поверхностей, объемов по заданным в условии задачи элементам;
- Сечения многогранников - методы построения сечений (например, метод следов) и нахождения площадей сечений и объемов получившихся после построения сечения многогранников (например, использование свойств перпендикулярной проекции и метод объемов).
При решении стереометрических задач более эффективным по сравнению с классическим методом нередко оказывается векторно-координатный. Классический метод решения задач требует отличного знания аксиом и теорем стереометрии, умения применять их на практике, строить чертежи пространственных тел и сводить стереометрическую задачу к цепочке планиметрических . Классический метод, как правило, быстрее приводит к искомому результату, чем векторно-координатный, но требует определенной гибкости мышления. Векторно-координатный метод представляет собой набор готовых формул и алгоритмов, но при этом требует более длительных расчетов; тем не менее, для некоторых задач, например, для нахождения углов в пространстве , он предпочтительнее классического.
Многим абитуриентам не позволяет справиться со стереометрической задачей неразвитое пространственное воображение . В этом случае мы рекомендуем использовать для самоподготовки интерактивные тренажеры с динамическими моделями пространственных тел. на портале «1С:Репетитор» (для перехода к их использованию необходимо зарегистрироваться): работая с ними, вы не только сможете «выстроить» решение задачи «по шагам», но и на объемной модели увидеть все этапы построения чертежа в различных ракурсах.
С помощью таких же динамических чертежей мы рекомендуем учиться строить сечения многогранников. Кроме того, что модель автоматически проверит правильность вашего построения, вы сами сможете, рассматривая сечение с разных сторон, убедиться, верно или неверно оно построено, и если неправильно, то в чем именно ошибка. Построение сечения на бумаге, с помощью карандаша и линейки, конечно, таких возможностей не дает. Посмотрите пример построения сечения пирамиды плоскостью с использованием такой модели (Нажмите на картинку, что бы перейти к тренажеру):
Последний вопрос, на который надо обратить внимание, - это нахождение площадей сечений или объемов , получившихся после построения сечения многогранников. Здесь также существуют подходы и теоремы, которые позволяют в общем случае существенно сократить трудозатраты на поиск решения и получение ответа. В курсе «1С:Репетитор» мы знакомим вас с этими приемами.
Если вы следовали нашим советам, разобрались со всеми вопросами, которые здесь затронуты, и решили достаточное количество задач, то велика вероятность, что вы практически готовы к решению задачи по стереометрии на профильном ЕГЭ по математике в 2018 году. Дальше необходимо только поддерживать себя «в форме» до самого экзамена, то есть решать, решать и решать задачи, совершенствуя свое умение применять изученные приемы и методы в разных ситуациях. Удачи!
Регулярно тренируйтесь в решении задач
Чтобы начать заниматься на портале «1С:Репетитор», достаточно .
Вы можете:
- заниматься самостоятельно и бесплатно , используя учебные материалы, включающие комплекс видеоуроков, пошаговых тренажеров и онлайн-тестов по каждой теме ЕГЭ;
- воспользоваться более эффективным (с учетом особенностей восприятия учащихся) средством: пройти, , на которых будут детально разбираться теория и способы решения задач ЕГЭ по математике.
В 2017 году мы провели серию вебинаров, посвященный рациональным уравнениям и неравенствам. Записи вебинаров будут доступны пользователям, оформившим подписку на весь курс 9900₽ 7900₽ . Для пробы можете купить доступ на один месяц за 990 ₽
Здесь ключевые фразы, чтобы поисковые роботы лучше находили наши советы:
Как решать задание 14 на экзамене ЕГЭ, задачи по геометрии, решение задач, по стереометрии, методы решения задач, тренажеры, видео, КИМ ЕГЭ 2017, подготовка к ЕГЭ, профиль математика, математика профильного уровня, решение задачи по наклонной треугольной призме, грани, взаимно перпендикулярно, общее ребро, плоскости, точки, ребро равно, боковая поверхность, решение задач на сечение многогранника, перпендикулярное сечение, вычислить объем фигуры, в основании прямой треугольной призмы лежит, признаки равенства и подобия треугольников, примеры решения задач ЕГЭ по геометрии, вычисление сечения, задачи по математике профильного уровня, применение методов сечения, решение задач на площадь, задачи ЕГЭ 2017 по стереометрии, подготовка к ЕГЭ, выпускникам 11 класса, в 2018 году, поступающим в технический вуз.
Среднее общее образование
Линия УМК Г. К. Муравина. Алгебра и начала математического анализа (10-11) (углуб.)
Линия УМК Мерзляка. Алгебра и начала анализа (10-11) (У)
Математика
Подготовка к ЕГЭ по математике (профильный уровень): задания, решения и объяснения
Разбираем задания и решаем примеры с учителемЭкзаменационная работа профильного уровня длится 3 часа 55 минут (235 минут).
Минимальный порог - 27 баллов.
Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности и числу заданий.
Определяющим признаком каждой части работы является форма заданий:
- часть 1 содержит 8 заданий (задания 1-8) с кратким ответом в виде целого числа или конечной десятичной дроби;
- часть 2 содержит 4 задания (задания 9-12) с кратким ответом в виде целого числа или конечной десятичной дроби и 7 заданий (задания 13–19) с развернутым ответом (полная запись решения с обоснованием выполненных действий).
Панова Светлана Анатольевна , учитель математики высшей категории школы, стаж работы 20 лет:
«Для того чтобы получить школьный аттестат, выпускнику необходимо сдать два обязательных экзамена в форме ЕГЭ, один из которых математика. В соответствии с Концепцией развития математического образования в Российской Федерации ЕГЭ по математике разделен на два уровня: базовый и профильный. Сегодня мы рассмотрим варианты профильного уровня».
Задание № 1 - проверяет у участников ЕГЭ умение применять навыки, полученные в курсе 5 - 9 классов по элементарной математике, в практической деятельности. Участник должен владеть вычислительными навыками, уметь работать с рациональными числами, уметь округлять десятичные дроби, уметь переводить одни единицы измерения в другие.
Пример 1. В квартире, где проживает Петр, установили прибор учета расхода холодной воды (счетчик). Первого мая счетчик показывал расход 172 куб. м воды, а первого июня - 177 куб. м. Какую сумму должен заплатить Петр за холодную воду за май, если цена 1 куб. м холодной воды составляет 34 руб 17 коп? Ответ дайте в рублях.
Решение:
1) Найдем количество потраченной воды за месяц:
177 - 172 = 5 (куб м)
2) Найдем сколько денег заплатят за потраченную воду:
34,17 · 5 = 170,85 (руб)
Ответ: 170,85.
Задание № 2 -является одним из простейших заданий экзамена. С ней успешно справляется большинство выпускников, что свидетельствует о владении определением понятия функции. Тип задания № 2 по кодификатору требований - это задание на использования приобретённых знаний и умений в практической деятельности и повседневной жизни. Задание № 2 состоит из описания с помощью функций различных реальных зависимостей между величинами и интерпретация их графиков. Задание № 2 проверяет умение извлекать информацию, представленную в таблицах, на диаграммах, графиках. Выпускникам нужно уметь определять значение функции по значению аргумента при различных способах задания функции и описывать поведение и свойства функции по её графику. Также необходимо уметь находить по графику функции наибольшее или наименьшее значение и строить графики изученных функций. Допускаемые ошибки носят случайный характер в чтении условия задачи, чтении диаграммы.
#ADVERTISING_INSERT#
Пример 2. На рисунке показано изменение биржевой стоимости одной акции добывающей компании в первой половине апреля 2017 года. 7 апреля бизнесмен приобрёл 1000 акций этой компании. 10 апреля он продал три четверти купленных акций, а 13 апреля продал все оставшиеся. Сколько потерял бизнесмен в результате этих операций?

Решение:
2) 1000 · 3/4 = 750 (акций) - составляют 3/4 от всех купленных акций.
6) 247500 + 77500 = 325000 (руб) - бизнесмен получил после продажи 1000 акций.
7) 340000 – 325000 = 15000 (руб) - потерял бизнесмен в результате всех операций.
Ответ: 15000.
Задание № 3 - является заданием базового уровня первой части, проверяет умения выполнять действия с геометрическими фигурами по содержанию курса «Планиметрия». В задании 3 проверяется умение вычислять площадь фигуры на клетчатой бумаге, умение вычислять градусные меры углов, вычислять периметры и т.п.
Пример 3. Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Решение: Для вычисления площади данной фигуры можно воспользоваться формулой Пика:
Для вычисления площади данного прямоугольника воспользуемся формулой Пика:
|
S = В + |
Г | |
| 2 |
|
S = 18 + |
6 | |
| 2 |

Читайте также: ЕГЭ по физике: решение задач о колебаниях
Задание № 4 - задача курса «Теория вероятностей и статистика». Проверяется умение вычислять вероятность события в простейшей ситуации.
Пример 4. На окружности отмечены 5 красных и 1 синяя точка. Определите, каких многоугольников больше: тех, у которых все вершины красные, или тех, у которых одна из вершин синяя. В ответе укажите, на сколько одних больше, чем других.
Решение: 1) Воспользуемся формулой числа сочетаний из n элементов по k :
у которых все вершины красные.
3) Один пятиугольник, у которого все вершины красные.
4) 10 + 5 + 1 = 16 многоугольников, у которых все вершины красные.
у которых вершины красные или с одной синей вершиной.
у которых вершины красные или с одной синей вершиной.
8) Один шестиуголник, у которого вершины красные с одной синей вершиной.
9) 20 + 15 + 6 + 1 = 42 многоуголника, у которых все вершины красные или с одной синей вершиной.
10) 42 – 16 = 26 многоугольников, в которых используется синяя точка.
11) 26 – 16 = 10 многоугольников – на сколько многоугольников, у которых одна из вершин - синяя точка, больше, чем многоугольников, у которых все вершины только красные.
Ответ: 10.
Задание № 5 - базового уровня первой части проверяет умения решать простейшие уравнения (иррациональные, показательные, тригонометрические, логарифмические).
Пример 5. Решите уравнение 2 3 + x = 0,4 · 5 3 + x .
Решение. Разделим обе части данного уравнения на 5 3 + х ≠ 0, получим
| 2 3 + x | = 0,4 или | 2 | 3 + х | = | 2 | , | ||
| 5 3 + х | 5 | 5 |
откуда следует, что 3 + x = 1, x = –2.
Ответ: –2.
Задание № 6 по планиметрии на нахождение геометрических величин (длин, углов, площадей), моделирование реальных ситуаций на языке геометрии. Исследование построенных моделей с использованием геометрических понятий и теорем. Источником трудностей является, как правило, незнание или неверное применение необходимых теорем планиметрии.
Площадь треугольника ABC равна 129. DE – средняя линия, параллельная стороне AB . Найдите площадь трапеции ABED .

Решение. Треугольник CDE подобен треугольнику CAB по двум углам, так как угол при вершине C общий, угол СDE равен углу CAB как соответственные углы при DE || AB секущей AC . Так как DE – средняя линия треугольника по условию, то по свойству средней линии | DE = (1/2)AB . Значит, коэффициент подобия равен 0,5. Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому
Следовательно, S ABED = S ΔABC – S ΔCDE = 129 – 32,25 = 96,75.
Задание № 7 - проверяет применение производной к исследованию функции. Для успешного выполнения необходимо содержательное, не формальное владение понятием производной.
Пример 7. К графику функции y = f (x ) в точке с абсциссой x 0 проведена касательная, которая перпендикулярна прямой, проходящей через точки (4; 3) и (3; –1) этого графика. Найдите f ′(x 0).
Решение. 1) Воспользуемся уравнением прямой, проходящей через две заданные точки и найдём уравнение прямой, проходящей через точки (4; 3) и (3; –1).
(y – y 1)(x 2 – x 1) = (x – x 1)(y 2 – y 1)
(y – 3)(3 – 4) = (x – 4)(–1 – 3)
(y – 3)(–1) = (x – 4)(–4)
–y + 3 = –4x + 16| · (–1)
y – 3 = 4x – 16
y = 4x – 13, где k 1 = 4.
2) Найдём угловой коэффициент касательной k 2 , которая перпендикулярна прямой y = 4x – 13, где k 1 = 4, по формуле:
3) Угловой коэффициент касательной – производная функции в точке касания. Значит, f ′(x 0) = k 2 = –0,25.
Ответ: –0,25.
Задание № 8 - проверяет у участников экзамена знания по элементарной стереометрии, умение применять формулы нахождения площадей поверхностей и объемов фигур, двугранных углов, сравнивать объемы подобных фигур, уметь выполнять действия с геометрическими фигурами, координатами и векторами и т.п.
Объём куба, описанного около сферы, равен 216. Найдите радиус сферы.

Решение. 1) V куба = a 3 (где а – длина ребра куба), поэтому
а 3 = 216
а = 3 √216
2) Так как сфера вписана в куб, значит, длина диаметра сферы равна длине ребра куба, поэтому d = a , d = 6, d = 2R , R = 6: 2 = 3.
Задание № 9 - требует от выпускника навыков преобразования и упрощения алгебраических выражений. Задание № 9 повышенного уровня сложности с кратким ответом. Задания из раздела «Вычисления и преобразования» в ЕГЭ подразделяются на несколько видов:
- преобразования числовых/буквенных тригонометрических выражений.
преобразования числовых рациональных выражений;
преобразования алгебраических выражений и дробей;
преобразования числовых/буквенных иррациональных выражений;
действия со степенями;
преобразование логарифмических выражений;
Пример 9. Вычислите tgα, если известно, что cos2α = 0,6 и
| 3π | < α < π. |
| 4 |
Решение. 1) Воспользуемся формулой двойного аргумента: cos2α = 2 cos 2 α – 1 и найдём
| tg 2 α = | 1 | – 1 = | 1 | – 1 = | 10 | – 1 = | 5 | – 1 = 1 | 1 | – 1 = | 1 | = 0,25. |
| cos 2 α | 0,8 | 8 | 4 | 4 | 4 |
Значит, tg 2 α = ± 0,5.
3) По условию
| 3π | < α < π, |
| 4 |
значит, α – угол II четверти и tgα < 0, поэтому tgα = –0,5.
Ответ: –0,5.
#ADVERTISING_INSERT# Задание № 10 - проверяет у учащихся умение использовать приобретенные раннее знания и умения в практической деятельности и повседневной жизни. Можно сказать, что это задачи по физике, а не по математике, но все необходимые формулы и величины даны в условии. Задачи сводятся к решению линейного или квадратного уравнения, либо линейного или квадратного неравенства. Поэтому необходимо уметь решать такие уравнения и неравенства, и определять ответ. Ответ должен получиться в виде целого числа или конечной десятичной дроби.
Два тела массой m
= 2 кг каждое, движутся с одинаковой скоростью v
= 10 м/с под углом 2α
друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении определяется выражением Q
= mv
2 sin 2 α. Под каким наименьшим углом 2α
(в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 50 джоулей?
Решение.
Для решения задачи нам необходимо решить неравенство Q ≥ 50, на интервале 2α
∈ (0°; 180°).
mv 2 sin 2 α ≥ 50
2· 10 2 sin 2 α ≥ 50
200 · sin 2 α ≥ 50
Так как α ∈ (0°; 90°), то будем решать только
Изобразим решение неравенства графически:

Так как по условию α ∈ (0°; 90°), значит 30° ≤ α < 90°. Получили, что наименьший угол α равен 30°, тогда наименьший угол 2α = 60°.
Задание № 11 - является типовым, но оказывается непростым для учащихся. Главным источником затруднений является построение математической модели (составление уравнения). Задание № 11 проверяет умение решать текстовые задачи.
Пример 11. На весенних каникулах 11-классник Вася должен был решить 560 тренировочных задач для подготовки к ЕГЭ. 18 марта в последний учебный день Вася решил 5 задач. Далее ежедневно он решал на одно и то же количество задач больше по сравнению с предыдущим днём. Определите, сколько задач Вася решил 2 апреля в последний день каникул.
Решение: Обозначим a 1 = 5 – количество задач, которые Вася решил 18 марта, d – ежедневное количество задач, решаемых Васей, n = 16 – количество дней с 18 марта по 2 апреля включительно, S 16 = 560 – общее количество задач, a 16 – количество задач, которые Вася решил 2 апреля. Зная, что ежедневно Вася решал на одно и то же количество задач больше по сравнению с предыдущим днём, то можно использовать формулы нахождения суммы арифметической прогрессии:560 = (5 + a 16) · 8,
5 + a 16 = 560: 8,
5 + a 16 = 70,
a 16 = 70 – 5
a 16 = 65.
Ответ: 65.
Задание № 12 - проверяют у учащихся умение выполнять действия с функциями, уметь применять производную к исследованию функции.
Найти точку максимума функции y = 10ln(x + 9) – 10x + 1.
Решение: 1) Найдем область определения функции: x + 9 > 0, x > –9, то есть x ∈ (–9; ∞).
2) Найдем производную функции:
4) Найденная точка принадлежит промежутку (–9; ∞). Определим знаки производной функции и изобразим на рисунке поведение функции:

Искомая точка максимума x = –8.
Скачать бесплатно рабочую программу по математике к линии УМК Г.К. Муравина, К.С. Муравина, О.В. Муравиной 10-11 Скачать бесплатно методические пособия по алгебреЗадание № 13 -повышенного уровня сложности с развернутым ответом, проверяющее умение решать уравнения, наиболее успешно решаемое среди заданий с развернутым ответом повышенного уровня сложности.
а) Решите уравнение 2log 3 2 (2cosx ) – 5log 3 (2cosx ) + 2 = 0
б) Найдите все корни этого уравнения, принадлежащие отрезку .
Решение: а) Пусть log 3 (2cosx ) = t , тогда 2t 2 – 5t + 2 = 0,
|
|
log 3 (2cosx ) = | 2 | ⇔ |
|
2cosx = 9 | ⇔ |
|
cosx = | 4,5 | ⇔ т.к. |cosx | ≤ 1, |
| log 3 (2cosx ) = | 1 | 2cosx = √3 | cosx = | √3 | ||||||
| 2 | 2 |
| то cosx = | √3 |
| 2 |
|
|
x = | π | + 2πk |
| 6 | |||
| x = – | π | + 2πk , k ∈ Z | |
| 6 |
б) Найдём корни, лежащие на отрезке .

Из рисунка видно, что заданному отрезку принадлежат корни
| 11π | и | 13π | . |
| 6 | 6 |
| Ответ: а) | π | + 2πk ; – | π | + 2πk , k ∈ Z ; б) | 11π | ; | 13π | . |
| 6 | 6 | 6 | 6 |
Диаметр окружности основания цилиндра равен 20, образующая цилиндра равна 28. Плоскость пересекает его основания по хордам длины 12 и 16. Расстояние между хордами равно 2√197.
а) Докажите, что центры оснований цилиндра лежат по одну сторону от этой плоскости.
б) Найдите угол между этой плоскостью и плоскостью основания цилиндра.
Решение: а) Хорда длиной 12 находится на расстоянии = 8 от центра окружности основания, а хорда длиной 16, аналогично, – на расстоянии 6. Поэтому расстояние между их проекциями на плоскость, параллельную основаниям цилиндров, составляет либо 8 + 6 = 14, либо 8 − 6 = 2.

Тогда расстояние между хордами составляет либо
= = √980 = = 2√245
= = √788 = = 2√197.
По условию реализовался второй случай, в нем проекции хорд лежат по одну сторону от оси цилиндра. Значит, ось не пересекает данную плоскость в пределах цилиндра, то есть основания лежат по одну сторону от нее. Что требовалось доказать.
б) Обозначим центры оснований за О 1 и О 2 . Проведем из центра основания с хордой длины 12 серединный перпендикуляр к этой хорде (он имеет длину 8, как уже отмечалось) и из центра другого основания - к другой хорде. Они лежат в одной плоскости β, перпендикулярной этим хордам. Назовем середину меньшей хорды B, большей A и проекцию A на второе основание - H (H ∈ β). Тогда AB,AH ∈ β и значит, AB,AH перпендикулярны хорде, то есть прямой пересечения основания с данной плоскостью.
Значит, искомый угол равен
| ∠ABH = arctg | AH | = arctg | 28 | = arctg14. |
| BH | 8 – 6 |
Задание № 15 - повышенного уровня сложности с развернутым ответом, проверяет умение решать неравенства, наиболее успешно решаемое среди заданий с развернутым ответом повышенного уровня сложности.
Пример 15. Решите неравенство |x 2 – 3x | · log 2 (x + 1) ≤ 3x – x 2 .
Решение: Областью определения данного неравенства является интервал (–1; +∞). Рассмотри отдельно три случая:
1) Пусть x 2 – 3x = 0, т.е. х = 0 или х = 3. В этом случае данное неравенство превращается в верное, следовательно, эти значения входят в решение.
2) Пусть теперь x 2 – 3x > 0, т.е. x ∈ (–1; 0) ∪ (3; +∞). При этом данное неравенство можно переписать в виде (x 2 – 3x ) · log 2 (x + 1) ≤ 3x – x 2 и разделить на положительное выражение x 2 – 3x . Получим log 2 (x + 1) ≤ –1, x + 1 ≤ 2 –1 , x ≤ 0,5 –1 или x ≤ –0,5. Учитывая область определения, имеем x ∈ (–1; –0,5].
3) Наконец, рассмотрим x 2 – 3x < 0, при этом x ∈ (0; 3). При этом исходное неравенство перепишется в виде (3x – x 2) · log 2 (x + 1) ≤ 3x – x 2 . После деления на положительное выражение 3x – x 2 , получим log 2 (x + 1) ≤ 1, x + 1 ≤ 2, x ≤ 1. Учитывая область, имеем x ∈ (0; 1].
Объединяя полученные решения, получаем x ∈ (–1; –0.5] ∪ ∪ {3}.
Ответ: (–1; –0.5] ∪ ∪ {3}.
Задание № 16 - повышенного уровня относится к заданиям второй части с развернутым ответом. Задание проверяет умения выполнять действия с геометрическими фигурами, координатами и векторами. Задание содержит два пункта. В первом пункте задание нужно доказать, а во втором пункте вычислить.
В равнобедренном треугольнике ABC с углом 120° при вершине A проведена биссектриса BD. В треугольник ABC вписан прямоугольник DEFH так, что сторона FH лежит на отрезке BC, а вершина E – на отрезке AB. а) Докажите, что FH = 2DH. б) Найдите площадь прямоугольника DEFH, если AB = 4.
Решение: а)

1) ΔBEF – прямоугольный, EF⊥BC, ∠B = (180° – 120°) : 2 = 30°, тогда EF = BE по свойству катета, лежащего против угла 30°.
2) Пусть EF = DH = x , тогда BE = 2x , BF = x √3 по теореме Пифагора.
3) Так как ΔABC равнобедренный, значит, ∠B = ∠C = 30˚.
BD – биссектриса ∠B, значит ∠ABD = ∠DBC = 15˚.
4) Рассмотрим ΔDBH – прямоугольный, т.к. DH⊥BC.
| 2x | = | 4 – 2x |
| 2x (√3 + 1) | 4 |
| 1 | = | 2 – x |
| √3 + 1 | 2 |
√3 – 1 = 2 – x
x = 3 – √3
EF = 3 – √3
2) S DEFH = ED · EF = (3 – √3 ) · 2(3 – √3 )
S DEFH = 24 – 12√3.
Ответ: 24 – 12√3.
Задание № 17 - задание с развернутым ответом, это задание проверяет применение знаний и умений в практической деятельности и повседневной жизни, умение строить и исследовать математические модели. Это задание - текстовая задача с экономическим содержанием.
Пример 17. Вклад в размере 20 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме того, в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на х млн. рублей, где х - целое число. Найдите наибольшее значение х , при котором банк за четыре года начислит на вклад меньше 17 млн рублей.
Решение: В конце первого года вклад составит 20 + 20 · 0,1 = 22 млн рублей, а в конце второго – 22 + 22 · 0,1 = 24,2 млн рублей. В начале третьего года вклад (в млн рублей) составит (24,2 + х ), а в конце - (24,2 + х) + (24,2 + х) · 0,1 = (26,62 + 1,1х ). В начале четвёртого года вклад составит (26,62 + 2,1х) , а в конце - (26,62 + 2,1х ) + (26,62 + 2,1х ) · 0,1 = (29,282 + 2,31х ). По условию, нужно найти наибольшее целое х, для которого выполнено неравенство
(29,282 + 2,31x ) – 20 – 2x < 17
29,282 + 2,31x – 20 – 2x < 17
0,31x < 17 + 20 – 29,282
0,31x < 7,718
| x < | 7718 |
| 310 |
| x < | 3859 |
| 155 |
| x < 24 | 139 |
| 155 |
Наибольшее целое решение этого неравенства - число 24.
Ответ: 24.
Задание № 18 - задание повышенного уровня сложности с развернутым ответом. Это задание предназначено для конкурсного отбора в вузы с повышенными требованиями к математической подготовке абитуриентов. Задание высокого уровня сложности - это задание не на применение одного метода решения, а на комбинацию различных методов. Для успешного выполнения задания 18 необходим, кроме прочных математических знаний, также высокий уровень математической культуры.
При каких a система неравенств
| x 2 + y 2 ≤ 2ay – a 2 + 1 | |
| y + a ≤ |x | – a |
имеет ровно два решения?
Решение: Данную систему можно переписать в виде
| x 2 + (y – a ) 2 ≤ 1 | |
| y ≤ |x | – a |
Если нарисовать на плоскости множество решений первого неравенства, получится внутренность круга (с границей) радиуса 1 с центром в точке (0, а
). Множество решений второго неравенства – часть плоскости, лежащая под графиком функции y
= |
x
| –
a
,
причём последний есть график функции
y
= |
x
|
, сдвинутый вниз на а
. Решение данной системы есть пересечение множеств решений каждого из неравенств.
Следовательно, два решения данная система будет иметь лишь в случае, изображённом на рис. 1.

Точки касания круга с прямыми и будут двумя решениями системы. Каждая из прямых наклонена к осям под углом 45°. Значит, треугольник PQR – прямоугольный равнобедренный. Точка Q имеет координаты (0, а ), а точка R – координаты (0, –а ). Кроме того, отрезки PR и PQ равны радиусу окружности, равному 1. Значит,
| Qr = 2a = √2, a = | √2 | . |
| 2 |
| Ответ: a = | √2 | . |
| 2 |
Задание № 19 - задание повышенного уровня сложности с развернутым ответом. Это задание предназначено для конкурсного отбора в вузы с повышенными требованиями к математической подготовке абитуриентов. Задание высокого уровня сложности - это задание не на применение одного метода решения, а на комбинацию различных методов. Для успешного выполнения задания 19 необходимо уметь осуществлять поиск решения, выбирая различные подходы из числа известных, модифицируя изученные методы.
Пусть Sn сумма п членов арифметической прогрессии (а п ). Известно, что S n + 1 = 2n 2 – 21n – 23.
а) Укажите формулу п -го члена этой прогрессии.
б) Найдите наименьшую по модулю сумму S n .
в) Найдите наименьшее п , при котором S n будет квадратом целого числа.
Решение : а) Очевидно, что a n = S n – S n – 1 . Используя данную формулу, получаем:
S n = S (n – 1) + 1 = 2(n – 1) 2 – 21(n – 1) – 23 = 2n 2 – 25n ,
S n – 1 = S (n – 2) + 1 = 2(n – 1) 2 – 21(n – 2) – 23 = 2n 2 – 25n + 27
значит, a n = 2n 2 – 25n – (2n 2 – 29n + 27) = 4n – 27.
Б) Так как S n = 2n 2 – 25n , то рассмотрим функцию S (x ) = | 2x 2 – 25x| . Ее график можно увидеть на рисунке.

Очевидно, что наименьшее значение достигается в целочисленных точках, расположенных наиболее близко к нулям функции. Очевидно, что это точки х = 1, х = 12 и х = 13. Поскольку, S (1) = |S 1 | = |2 – 25| = 23, S (12) = |S 12 | = |2 · 144 – 25 · 12| = 12, S (13) = |S 13 | = |2 · 169 – 25 · 13| = 13, то наименьшее значение равно 12.
в) Из предыдущего пункта вытекает, что Sn положительно, начиная с n = 13. Так как S n = 2n 2 – 25n = n (2n – 25), то очевидный случай, когда данное выражение является полным квадратом, реализуется при n = 2n – 25, то есть при п = 25.
Осталось проверить значения с 13 до 25:
S 13 = 13 · 1, S 14 = 14 · 3, S 15 = 15 · 5, S 16 = 16 · 7, S 17 = 17 · 9, S 18 = 18 · 11, S 19 = 19 · 13, S 20 = 20 · 13, S 21 = 21 · 17, S 22 = 22 · 19, S 23 = 23 · 21, S 24 = 24 · 23.
Получается, что при меньших значениях п полный квадрат не достигается.
Ответ: а) a n = 4n – 27; б) 12; в) 25.
________________
*С мая 2017 года объединенная издательская группа «ДРОФА-ВЕНТАНА» входит в корпорацию «Российский учебник». В корпорацию также вошли издательство «Астрель» и цифровая образовательная платформа «LECTA». Генеральным директором назначен Александр Брычкин, выпускник Финансовой академии при Правительстве РФ, кандидат экономических наук, руководитель инновационных проектов издательства «ДРОФА» в сфере цифрового образования (электронные формы учебников, «Российская электронная школа», цифровая образовательная платформа LECTA). До прихода в издательство «ДРОФА» занимал позицию вице-президента по стратегическому развитию и инвестициям издательского холдинга «ЭКСМО-АСТ». Сегодня издательская корпорация «Российский учебник» обладает самым крупным портфелем учебников, включенных в Федеральный перечень - 485 наименований (примерно 40%, без учета учебников для коррекционной школы). Издательствам корпорации принадлежат наиболее востребованные российскими школами комплекты учебников по физике, черчению, биологии, химии, технологии, географии, астрономии - областям знаний, которые нужны для развития производственного потенциала страны. В портфель корпорации входят учебники и учебные пособия для начальной школы, удостоенные Премии Президента в области образования. Это учебники и пособия по предметным областям, которые необходимы для развития научно-технического и производственного потенциала России.
В задании №13 ЕГЭ по математике базового уровня придется продемонстрировать умения и знания одного из понятий поведения функции: производных в точке или скоростей возрастания или убывания. Теория к этому заданию будет добавлена чуть позже, но это не помешает нам подробно разобрать несколько типовых вариантов.
Разбор типовых вариантов заданий №14 ЕГЭ по математике базового уровня
Первый вариант задания (демонстрационный вариант 2018)
На графике изображена зависимость температуры от времени в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя; на вертикальной оси – температура двигателя в градусах Цельсия.
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.
В таблице под каждой буквой укажите соответствующий номер.
Алгоритм выполнения:
- Выбрать интервал времени, на котором температура падала.
- Приложить линейку к 30°С и определить интервал времени, на котором температура была ниже 30°С.
Решение:
Выберем интервал времени, на котором температура падала. Этот участок видно не вооруженным глазом, он начинается в 8 мин от момента запуска двигателя.
Приложим линейку к 30°С и определить интервал времени, на котором температура была ниже 30°С.

Ниже линейки окажется участок, соответствующий интервалу времени 0 – 1 мин.
С помощью карандаша и линейки найдем на каком интервале времени температура находилась в пределах от 40°С до 80°С.
Опустим из точек, соответствующих 40°С и 80°С перпендикуляры на график, а из полученных точек опустим перпендикуляры на ось времени.

Видим, что этому температурному интервалу соответствует интервал времени 3 – 6,5 мин. То есть из приведенных в условии 3 – 6 мин.
Методом исключения выберем недостающий вариант ответа.
Второй вариант задания
| ГРАФИКИ ФУНКЦИЙ
| ГРАФИКИ ПРОИЗВОДНЫХ
|
Решение:
Проанализируем график функции А. Если Функция возрастает, то производная положительна и наоборот. Производная функции равна нулю в точках экстремума.
Сначала функция А возрастает, т.е. производная положительна. Этому соответствуют графики производных 2 и 3. В точке максимума функции x=-2, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 3.
Сначала функция Б убывает, т.е. производная отрицательна. Этому соответствуют графики производных 1 и 4. Точка максимума функции x=-2, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 4.
Сначала функция В возрастает, т.е. производная положительна. Этому соответствуют графики производных 2 и 3. Точка максимума функции x = 1, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 2.
Методом исключения можем определить, что графику функции Г соответствует график производной под номером 1.
Ответ: 3421.
Третий вариант задания
Установите соответствие между графиками функций и графиками их производных.
| ГРАФИКИ ФУНКЦИЙ
| ГРАФИКИ ПРОИЗВОДНЫХ
|
Алгоритм выполнения для каждой из функций:
- Определить промежутки возрастания и убывания функций.
- Определить точки максимума и точки минимума функций.
- Сделать выводы, поставить в соответствие предложенные графики.
Решение:
Проанализируем график функции А.
Если функция возрастает, то производная положительна и наоборот. Производная функции равна нулю в точках экстремума.
Точка экстремума – это точка, в которой достигается максимальное или минимальное значение функции.
Сначала функция А возрастает, т.е. производная положительна. Этому соответствуют графики производных 3 и 4. В точке максимума функции x=0, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 4.
Проанализируем график функции Б.
Сначала функция Б убывает, т.е. производная отрицательна. Этому соответствуют графики производных 1 и 2. Точка минимума функции x=-1, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 2.
Проанализируем график функции В.
Сначала функция В убывает, т.е. производная отрицательна. Этому соответствуют графики производных 1 и 2. Точка минимума функции x = 0, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 1.
Методом исключения можем определить, что графику функции Г соответствует график производной под номером 3.
Ответ: 4213.
Вариант четырнадцатого задания 2017
На рисунке изображен график функции и касательные, проведённые к нему в точках с абсциссами А, В, С и D. В правом столбце указаны значения производной в точках А, В, С и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.

ТОЧКИ
А
В
С
D
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
1) –4
2) 3
3) 2/3
4) -1/2
Вспомним, что означает производная, а именно ее значение в точке - значение функции производной в точке равно тангенсу угла наклона (коэффициенту) касательной.
В ответах у нас есть два положительных, и два отрицательных варианта. Как мы помним, если коэффициент прямой (графика y = kx+ b ) положительный - то прямая возрастает, если же он отрицательный - то прямая убывает.
Возрастающих прямых у нас две - в точке A и D. Теперь вспомним, что же означает значение коэффициента k?
Коэффициент k показывает, насколько быстро возрастает или убывает функция (на самом деле коэффициент k сам является производной функции y = kx+ b).
Поэтому k = 2/3 соответствует более пологой прямой - D, а k = 3 - A.
Аналогично и в случае с отрицательными значениями: точке B соответствует более крутая прямая с k = - 4, а точке С - -1/2.
Вариант четырнадцатого задания 2019 года(1)
На рисунке точками показаны объемы месячных продаж обогревателей в магазине бытовой техники. По горизонтали указываются месяцы, по вертикали – количество проданных обогревателей. Для наглядности точки соединены линией.

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж обогревателей .

Алгоритм выполнения
Анализируем части графика, соответствующие разным временам года. Формулируем ситуации, отображенные на графике. Находим для них наиболее подходящие варианты ответов.
Решение:
Зимой кол-во продаж превысило 120 шт./мес., причем оно все время увеличивалось. Эта ситуация соответствует варианту ответа №3. Т.е. получаем: А–3 .
Весной продажи постепенно упали со 120 обогревателей за месяц до 50. Наиболее приближенным к этой формулировке является вариант №2. Имеем: Б–2 .
Летом кол-во продаж не менялась и была минимальной. 2-я часть этой формулировки не отражена в ответах, а для первой подходит только №4. Отсюда имеем: В–4 .
Осенью продажи росли, однако их кол-во ни в одном из месяцев не превысило 100 штук. Эта ситуация описана в варианте №1. Получаем: Г–1 .
Вариант четырнадцатого задания 2019 года(2)
На графике изображена зависимость скорости движения рейсового автобуса от времени. На вертикальной оси отмечена скорость автобуса в км/ч, на горизонтальной – время в минутах, прошедшее с начала движения автобуса.
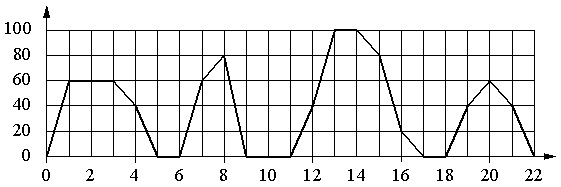
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику движения автобуса на этом интервале.

Алгоритм выполнения
- Определяем цену деления на горизонтальной и на вертикальной шкале.
- Анализируем по очереди предложенные утверждения 1–4 из правой колонки («Характеристики»). Сопоставляем их с временными интервалами из левой колонки таблицы, находим пары «буква–число» для ответа.
Решение:
Цена деления горизонтальной шкалы составляет 1 с, вертикальной – 20 км/ч.
- Когда автобус делает остановку, его скорость равна 0. Нулевую скорость в течение 2 минут подряд автобус имел только с 9-й по 11-ю минуту. Это время попадает в интервал 8–12 мин. Значит, имеем пару для ответа: Б–1 .
- Скорость 20 км/ч и больше автобус имел в течение нескольких временных промежутков. Причем вариант А здесь не подходит, т.к., к примеру, на 7-й минуте скорость составляла 60 км/ч, вариант Б – потому что он уже применен, вариант Г – потому что в начале и конце промежутка автобус имел нулевую скорость. В данном случае подходит вариант В (12–16 мин); на этом промежутке автобус начинает движение со скоростью 40 км/ч, далее ускоряется до 100 км/м и потом постепенно снижает скорость до 20 км/ч. Итак, имеем: В–2 .
- Здесь установлено ограничение для скорости. При этом варианты Б и В мы не рассматриваем. Оставшиеся же интервалы А и Г подходят оба. Поэтому правильно будет рассмотреть сначала 4-й вариант, а потом снова вернуться в 3-му.
- Из двух оставшихся интервалов для характеристики №4 подходит только 4–8 мин, поскольку на этом промежутке остановка была (на 6-й минуте). На промежутке 18–22 мин остановок не было. Получаем: А–4 . Отсюда следует, что для характеристики №3 нужно взять интервал Г, т.е. получается пара Г–3 .
Вариант четырнадцатого задания 2019 года(3)
На рисунке точками показан прирост населения Китая в период с 2004 по 2013 год. По горизонтали указывается год, по вертикали – прирост населения в процентах (увеличение численности населения относительно прошлого года). Для наглядности точки соединены линией.
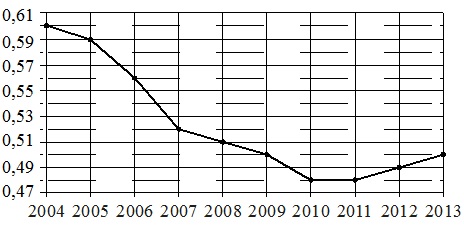
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику прироста населения Китая в этот период .

Алгоритм выполнения
- Определяем цену деления вертикальной шкалы рисунка. Находится она как разница пары соседних значений шкалы, деленная на 2 (т.к. между двумя соседними значениями имеется 2 деления).
- Анализируем последовательно приведенные в условии характеристики 1–4 (левая табличная колонка). Сопоставляем каждую из них с конкретным периодом времени (правая табличная колонка).
Решение:
Цена деления вертикальной шкалы составляет 0,01%.
- Падение прироста непрерывно продолжалось с 2004 по 2010 год. В 2010–2011 годах прирост был стабильно минимальным, и начиная с 2012 года оно начал увеличиваться. Т.е. остановка прироста произошла в 2010 году. Этот год находится в периоде 2009–2011 гг. Соответственно, имеем: В–1 .
- Наибольшим падением прироста следует считать самую «круто» падающую линию графика на рисунке. Она приходится на период 2006–2007 гг. и составляет 0,04%, за год (0,59–0,56=0,04% в 2006 г. и 0,56–0,52=0,04% в 2007 г.). Отсюда получаем: А–2 .
- Указанный в характеристике №3 прирост начался с 2007 года, продолжился в 2008 г. и завершился в 2009 году. Это соответствует периоду времени Б, т.е. имеем: Б–3 .
- Прирост населения начал увеличиваться после 2011 г., т.е. в 2012–2013 гг. Поэтому получаем: Г–4 .
Вариант четырнадцатого задания 2019 года(4)
На рисунке изображены график функции и касательные, проведенные к нему в точках с абсциссами А,В,С и D.

В правом столбце указаны значения производной функции в точках А, В, С и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.

Алгоритм выполнения
- Рассматриваем пару касательных, имеющих острый угол с положит.направлением оси абсцисс. Сравниваем их, находим соответствие среди пары соответствующих значений производных.
- Рассматриваем пару касательных, образующих с положит.направлением оси абсцисс тупой угол. Сравниваем их по модулю, определяем соответствие их значениям производных среди двух оставшихся в правой колонке.
Решение:
Острый угол с положит.направлением оси абсцисс образуют производные в т.В и т.С. Эти производные имеют положит.значения. Поэтому выбирать тут следует между значениями №№1 и 3. Применяя правило о том, что если угол меньше 45 0 , то производная меньше 1, а если больше, то больше 1, делаем вывод: в т.В производная по модулю больше 1, в т.С – меньше 1. Это означает, что можно составить пары для ответа: В–3 и С–1 .
Производные в т.А и т.D образуют с положит.направлением оси абсцисс тупой угол. И тут применяем то же правило, немного перефразировав его: чем больше касательная в точке «прижата» к линии оси абсцисс (к отрицат. ее направлению), тем больше она по модулю. Тогда получаем: производная в т.А по модулю меньше, чем производная в т.D. Отсюда имеем пары для ответа: А–2 и D–4 .
Вариант четырнадцатого задания 2019 года(5)
На рисунке точками показана среднесуточная температура воздуха в Москве в январе 2011 года. По горизонтали указываются числа месяца, по вертикали – температура в градусах Цельсия. Для наглядности точки соединены линией.

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику изменения температуры .

Алгоритм выполнения
Анализируем последовательно характеристики 1–4 (правая колонка), используя график на рисунке. Ставим каждой из них в соответствие конкретный временной период (левая колонка).
Решение:
- Рост температуры наблюдался только в конце периода 22–28 января. Здесь 27 и 28 числа она повышалась соответственно на 1 и на 2 градуса. В конце периода 1–7 января температура была стабильной (–10 градусов), в конце 8–14 и 15–21 января понижалась (с –1 до –2 и с –11 до –12 градусов соответственно). Поэтому получаем: Г–1 .
- Поскольку каждый временной период охватывает 7 дней, то анализировать нужно температуру, начиная с 4-го дня каждого периода. Неизменной в течение 3–4 дней температура была только с 4 по 7 января. Поэтому получаем ответ: А–2 .
- Месячный минимум температуры наблюдался 17 января. Это число входит в период 15–21 января. Отсюда имеем пару: В–3 .
- Температурный максимум пришелся 10 января и составил +1 градус. Эта дата попадает в период 8–14 января. Значит, имеем: Б–4.
Вариант четырнадцатого задания 2019 года(6)
На рисунке изображен график функции y=f(x) и отмечены точки А, В, С и D на оси Ох..

Пользуясь графиком, поставьте в соответствие каждой точке характеристики функции и ее производной

Алгоритм выполнения
- Значение функции в точке положительно, если эта точка расположена выше оси Ох.
- Производная в точке больше нуля, если касательная к этой точке образует острый угол с положительным направлением оси Ох.
Решение:
Точка А. Она находится ниже оси Ох, значит значение функции в ней отрицательно. Если провести в ней касательную, то угол между нею и положит.направлением Ох составит около 90 0 , т.е. образует острый угол. Значит, в данном случае подходит характеристика №3. Т.е. имеем: А–3 .
Точка Б. Она находится над осью Ох, т.е. точка имеет положит.значение функции. Касательная в этой точке будет довольно близко «прилегать» к оси абсцисс, образуя тупой угол (немногим меньше 180 0) с положительным ее направлением. Соответственно, производная в этой точке отрицательна. Т.о., здесь подходит характеристика 1. Получаем ответ: В–1 .
Точка С. Точка расположена ниже оси Ох, касательная в ней образует большой тупой угол с положит.направлением оси абсцисс. Т.е. в т.С значение и функции, и производной отрицательно, что соответствует характеристике №2. Ответ: С–2 .
Точка D. Точка находится выше оси Ох, а касательная в ней образует с положит.направлением оси острый угол. Это говорит о том, что как значение функции, так и значение производной здесь больше нуля. Ответ: D–4 .
Вариант четырнадцатого задания 2019 года(7)
На рисунке точками показаны объемы месячных продаж холодильников в магазине бытовой техники. По горизонтали указываются месяцы, по вертикали – количество проданных холодильников. Для наглядности точки соединены линией.

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж холодильников .

Алгоритм выполнения
- При необходимости найти кол-во холодильников за тот или иной период нужно определять их сумму за три месяца.
- Анализировать следует характеристики 1–4 (правая колонка), находя для каждой из них соответствие в виде временного периода (левая колонка).
Решение:
Анализируем характеристики:
- Меньше всего холодильников продано в начале и в конце года. Поэтому рассмотрим периоды январь–март и октябрь–декабрь. В январе–марте было продано примерно 250+250+300=800 холодильников, в октябре–декабре – примерно 350+200+100=650. Значит, здесь подходит все-таки последний период. Ответ: Г–1 .
- Длительный рост продаж наблюдался с апреля по июль. Это время охватывает полностью период апрель–июнь и захватывает начало следующего. Поэтому получаем: Б–2 .
- Тут тоже требуется найти сумму проданных единиц за целые периоды. Для 1-го и последнего периода она уже найдена (см.п.1). Считаем для 2-го и 3-го, получаем: 300+400+600=1300 – в апреле–июне, примерно 650+600+550=1800 – в июле–сентябре. К требуемым 800 холодильникам максимально приближен объем продаж в январе–марте. Поэтому имеем: А–3 .
- Одинаковое падение объема продаж означает, что разница между кол-вом проданных холодильников должна быть одинаковой. Падение продаж наблюдалось, начиная с конца июля. В августе падение составило 650–600=50 штук, в сентябре – 600–550=50 штук. Далее, в октябре, разница составила уже 550–350=200 холодильников, в ноябре 350–200=150, в декабре 200–100=100. Т.о., подходит в данном случаем период июль–сентябрь. Ответ: В–4 .
Вариант четырнадцатого задания 2019 года(8)
На рисунке точками показан годовой объем добычи угля в России открытым способом в период с 2001 по 2010 год. По горизонтали указывается год, по вертикали – объем добычи угля в миллионах тонн. Для наглядности точки соединены линиями.

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов характеристику добычи угля в этот период .

Алгоритм выполнения
- Точки, которые не приходятся на точные значения шкалы вертикальной оси, определяем приблизительно.
- Анализируем по очереди приведенные (в правом столбце) характеристики, используя данный график. Определяем соответствие каждой из них конкретного временного периода.
Анализируем характеристики:
- Объем добычи меньше 190 млн т приходился на период с 2001 года по 2005 год. Затем спад добычи зафиксирован в 2009 году, но один год не составляет периода. 2001–2005 годы полностью попадают в период А (2002–2004 гг.). Поэтому получаем ответ: А–1 .
- Такая формулировка «объем… сначала уменьшался, а затем начал расти» соответствует 2 периодам – 2002–2003 гг. и 2009–2010 гг. Но т.к. первый из этих периодов уже взят в качестве ответа, то правильно здесь использовать пару Г–2 .
- Ситуация, описанная в 3-й характеристике, наиболее точно отображена в периоде 2006–2008 гг. Именно в это время добыча сначала понемногу увеличивалась (примерно с 190 млн т до 210), а потом резко возросла до 250 млн т. Т.е. подходящий ответ здесь: 2006–2008 гг. и, соответственно, имеем: В–3 .
- Медленный рост следует искать в период, когда линия графика имеет наиболее пологий вид. Это: 2004–2006 год, что соответствует периоду Б, т.е. получаем: Б–4 .
Вариант четырнадцатого задания 2019 года(9)
На графике изображена зависимость температуры от времени в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси – температура двигателя в градусах Цельсия.

Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику температуры.

Алгоритм выполнения
Анализируем сначала очередную характеристику, а затем сопоставляем ее с конкретным временным интервалом.
Решение:
- Выше 60 0 температура была с 4-й по 7-ю минуту. Поэтому здесь нужно взять интервал 4–6 мин. Получаем: В–1 .
- Температура падала только после 7-й минуты. Соответственно, тут подходит интервал 7–9 мин. Ответ: Г–2 .
- Самый быстрый рост температуры происходил там, где график имеет наиболее «крутой» вертикальный подъем. Это имеет место только в 1-ю минуту нагревания. Т.е. подходящим интервалом является 0–1 мин. Ответ: А–3 .
- В пределах 40–50 0 С температура имела место, начиная со 2-й по 3-ю минуту. Значит, нужно выбрать интервал 2–3мин. Ответ: Б–4 .
Вариант четырнадцатого задания 2019 года(10)
На графике изображена зависимость частоты пульса гимнаста от времени в течение и после его выступления в вольных упражнениях. На горизонтальной оси отмечено время (в минутах), прошедшее с начала выступления гимнаста, на вертикальной оси – частота пульса (в ударах в минуту).

Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику пульса гимнаста на этом интервале.

Алгоритм выполнения
- Для анализа характеристики нужно использовать только 1-ю половину графика.
- Для точек графика, которые не попадают в «узлы» сетки рисунка (т.е. для которых невозможно определить точные значения), нужно определять значения приблизительно.
- Величина роста пульса связана с пологостью (или, напротив, крутизной) линии графика. Это означает, что чем большее изменение значения функции происходит за тот или иной (но обязательно одинаковый) промежуток времени, тем больше величина роста.
Решение:
Анализируем предложенные характеристики:
- Если частота пульса сначала падала, а затем росла, то на графике это должно выразиться в «прогибе» линии графика вниз. Такая кривизна наблюдается только в течение 3–4 минуты. Значит, получаем ответ: Г–1 .
- Самый большой «подъем» линии на 1-й половине графика имеет место с 1-й по 2-ю минуту. Отсюда получаем: Б–2 .
- Частота пульса падала, начиная со 2-й минуты. В течение 3–4 минут тоже наблюдалось падение, однако оно потом перешло в рост. Поэтому правильным здесь следует считать интервал В. Т.о., ответ: В–3 .
- Единственный интервал, на котором частота не превысила 100 ударов, – 0–1 мин. Отсюда имеем ответ: А–4 .








