МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ
Актуальность. Исторически сложилось, что тригонометрическим уравнениям и неравенствам уделялось особое место в школьном курсе. Можно сказать, что тригонометрия является одним из важнейших разделов школьного курса и всей математической науки в целом.
Тригонометрические уравнения и неравенства занимают одно из центральных мест в курсе математики средней школы, как по содержанию учебного материала, так и по способам учебно-познавательной деятельности, которые могут и должны быть сформированы при их изучении и применены к решению большого числа задач теоретического и прикладного характера.
Решение тригонометрических уравнений и неравенств создаёт предпосылки для систематизации знаний учащихся, связанных со всем учебным материалом по тригонометрии (например, свойства тригонометрических функций, приёмы преобразования тригонометрических выражений и т.д.) и даёт возможность установить действенные связи с изученным материалом по алгебре (уравнения, равносильность уравнений, неравенства, тождественные преобразования алгебраических выражений и т.д.).
Иначе говоря, рассмотрение приёмов решения тригонометрических уравнений и неравенств предполагает своего рода перенос этих умений на новое содержание.
Значимость теории и ее многочисленные применения являются доказательством актуальности выбранной темы. Это в свою очередь позволяет определить цели, задачи и предмет исследования курсовой работы.
Цель исследования: обобщить имеющиеся типы тригонометрических неравенств, основные и специальные методы их решения, подобрать комплекс задач для решения тригонометрических неравенств школьниками.
Задачи исследования:
1. На основе анализа имеющейся литературы по теме исследования систематизировать материал.
2. Привести комплекс заданий, необходимый для закрепления темы «Тригонометрические неравенства».
Объектом исследования являются тригонометрические неравенства в школьном курсе математики.
Предмет исследования: типы тригонометрических неравенств и методы их решения.
Теоретическая значимость заключается в систематизации материала.
Практическая значимость: применение теоретических знаний в решении задач; разбор основных часто встречающихся методов решений тригонометрических неравенств.
Методы исследования : анализ научной литературы, синтез и обобщение полученных знаний, анализ решения заданий, поиск оптимального методов решения неравенств.
§1. Типы тригонометрических неравенств и основные методы их решения
1.1. Простейшие тригонометрические неравенства
Два тригонометрических выражения, соединённые между собой знаком или >, называются тригонометрическими неравенствами.
Решить тригонометрическое неравенство – это значит, найти множество значений неизвестных, входящих в неравенство, при которых неравенство выполняется.
Основная часть тригонометрических неравенств решается сведением их к решению простейших:
Это может быть метод разложения на множители, замены переменного (
, 
и т.д.), где сначала решается обычное неравенство, а затем неравенство вида 
и т.д., или другие способы.
Простейшие неравенства решаются двумя способами: с помощью единичной окружности или графически.
Пусть
f(х
– одна из основных тригонометрических функций. Для решения неравенства 
достаточно найти его решение на одном периоде, т.е. на любом отрезке, длина которого равна периоду функции
f
x
. Тогда решением исходного неравенства будут все найденные
x
, а также те значения, которые отличаются от найденных на любое целое число периодов функции. При этом удобно использовать графический метод.
Приведем пример алгоритма решения неравенств
(
) и
.
Алгоритм решения неравенства
(
).
1. Сформулируйте определение синуса числа x на единичной окружности.
3. На оси ординат отметьте точку с координатой a .
4. Через данную точку проведите прямую, параллельную оси OX, и отметьте точки пересечения ее с окружностью.
5. Выделите дугу окружности, все точки которой имеют ординату, меньшую a .
6. Укажите направление обхода (против часовой стрелки) и запишите ответ, добавив к концам промежутка период функции
2πn
,
.
Алгоритм решения неравенства
.
1. Сформулируйте определение тангенса числа x на единичной окружности.
2. Нарисуйте единичную окружность.
3. Проведите линию тангенсов и на ней отметьте точку с ординатой a .
4. Соедините данную точку с началом координат и отметьте точку пересечения полученного отрезка с единичной окружностью.
5. Выделите дугу окружности, все точки которой имеют на линии тангенсов ординату, меньшую a .
6. Укажите направление обхода и запишите ответ с учетом области определения функции, добавив период
πn
,
(число, стоящее в записи слева, всегда меньше числа, стоящего справа).
Графическая интерпретация решений простейших уравнений и формулы решения неравенств в общем виде указаны в приложении (Приложения 1 и 2).
Пример 1.
Решите неравенство
.
На единичной окружности проводим прямую
, которая пересекает окружность в точках A и B.
Все значения
y
на промежутке NM больше
, все точки дуги AMB удовлетворяют данному неравенству. При всех углах поворота, больших
, но меньших
,
будет принимать значения больше
(но не больше единицы).
Рис.1
Таким образом, решением неравенства будут все значения на интервале
, т.е.
. Для того, чтобы получить все решения данного неравенства, достаточно к концам этого промежутка прибавить
, где
, т.е.
,
.
Заметим, что значения
и
являются корнями уравнения
,
т.е.
;
.
Ответ:
, .
1.2. Графический метод
На практике довольно часто оказывается полезным графический метод решения тригонометрических неравенств. Рассмотрим сущность метода на примере неравенства 
:
1. Если аргумент – сложный (отличен от х ), то заменяем его на t .
2. Строим в одной координатной плоскости
tOy
графики функций 
и 
.
3. Находим такие
две соседние точки пересечения графиков
, между которыми
синусоида
располагается
выше
прямой
. Находим абсциссы этих точек.
4. Записываем двойное неравенство для аргумента t , учитывая период косинуса (t будет между найденными абсциссами).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.
Пример 2. Решить неравенство: .
При решении неравенств графическим методом необходимо как можно более точно построить графики функций. Преобразуем неравенство к виду:
Построим в одной системе координат графики функций 
и 
(рис. 2).
Рис.2
Графики функций пересекаются в точке
А
с координатами 
; 
. На промежутке 
точки графика 
ниже точек графика 
. А при значения функции совпадают. Поэтому при 
.
Ответ: 
.
1.3. Алгебраический метод
Довольно часто исходное тригонометрическое неравенство путем удачно выбранной подстановки удается свести к алгебраическому (рациональному или иррациональному) неравенству. Данный метод подразумевает преобразование неравенства, введение подстановки или замену переменной.
Рассмотрим на конкретных примерах применение этого метода.
Пример 3.
Приведение к простейшему виду
.
(рис. 3)
Рис.3
, 
.
Ответ: 
,
Пример 4. Решить неравенство:
ОДЗ: 
, 
.
Используя формулы: 
, 
запишем неравенство в виде: 
.
Или, полагая 
после несложных преобразований получим
,
,
.
Решая последнее неравенство методом интервалов, получаем:
Рис.4
, соответственно 
. Тогда из рис. 4 следует 
, где 
.
Рис.5
Ответ:
, 
.
1.4. Метод интервалов
Общая схема решения тригонометрических неравенств методом интервалов:
С помощью тригонометрических формул разложить на множители.
Найти точки разрыва и нули функции, поставить их на окружность.
Взять любую точку К (но не найденную ранее) и выяснить знак произведения. Если произведение положительно, то поставить точку за единичной окружностью на луче, соответствующему углу. Иначе точку поставить внутри окружности.
Если точка встречается четное число раз, назовем ее точкой четной кратности, если нечетное число раз – точкой нечетной кратности. Провести дуги следующим образом: начать с точки К , если следующая точка нечетной кратности, то дуга пересекает окружность в этой точке, если же точка четной кратности, то не пересекает.
Дуги за окружностью – положительные промежутки; внутри окружности – отрицательные промежутки.
Пример 5. Решить неравенство
, 
.
Точки первой серии: 
.
Точки второй серии: 
.
Каждая точка встречается нечетное число раз, то есть все точки нечетной кратности.
Выясним знак произведения при 
: . Отметим все точки на единичной окружности (рис.6):
Рис. 6
Ответ: 
, 
; 
, 
; 
, 
.
Пример 6 . Решите неравенство .
Решение:
Найдём нули выражения .
Получ ae м :
,
;
, 
;
, 
;
, 
;
На единичной окружности значения серии
х
1
представлены точками 
. Серия
х
2
дает точки 
. Из серии
х
3
получаем две точки 
. Наконец, серию
х
4
будут представлять точки 
. Нанесем все эти точки на единичную окружность, указав в скобках рядом с каждой из них ее кратность.
Пусть теперь число 
будет равным. Делаем прикидку по знаку:
Значит, точку
A
следует выбрать на луче, образующем угол 
с лучом
Ох,
вне единичной окружности. (Заметим, что вспомогательный луч
О
A
совсем не обязательно изображать на рисунке. Точка
A
выбирается приблизительно.)
Теперь от точки
A
ведем волнообразную непрерывную линию последовательно ко всем отмеченным точкам. Причем в точках наша линия переходит из одной области в другую: если она находилась вне единичной окружности, то переходит внутрь нее. Подойдя к точке 
, линия возвращается во внутреннюю область, так как кратность этой точки четная. Аналогично в точке 
(с четной кратностью) линию приходится повернуть во внешнюю область. Итак, начертили некую картинку, изображенную на рис. 7. Она помогает выделить на единичной окружности искомые области. Они обозначены знаком « + ».
Рис.7
Окончательный ответ:
Примечание. Если волнообразную линию после обхода ею всех отмеченных на единичной окружности точек не удается вернуть в точку A , не пересекая окружность в «незаконном» месте, то это означает, что в решении допущена ошибка, а именно пропущено нечетное количество корней.
Ответ : .
§2. Комплекс задач по решению тригонометрических неравенств
В процессе формирования у школьников умений решать тригонометрические неравенства, также можно выделить 3 этапа.
1. подготовительный,
2. формирование умений решать простейшие тригонометрические неравенства;
3. введение тригонометрических неравенств других видов.
Цель подготовительного этапа состоит в том, что необходимо сформировать у школьников умение использовать тригонометрический круг или график для решения неравенств, а именно:
Умения решать простейшие неравенства вида
,
, ,
,
с помощью свойств функций синус и косинус;
Умения составлять двойные неравенства для дуг числовой окружности или для дуг графиков функций;
Умения выполнять различные преобразования тригонометрических выражений.
Реализовать этот этап рекомендуется в процессе систематизации знаний школьников о свойствах тригонометрических функций. Основным средством могут служить задания, предлагаемые учащимся и выполняемые либо под руководством учителя, либо самостоятельно, а так же навыки наработанные при решении тригонометрических уравнений.
Приведем примеры таких заданий:
1
. Отметьте на единичной окружности точку
, если
.
2.
В какой четверти координатной плоскости расположена точка
, если
равно:
3.
Отметьте на тригонометрической окружности точки
, если:
4. Приведите выражение к тригонометрическим функциям I четверти.
а)
,
б)
,
в)
5. Дана дуга МР. М – середина I -ой четверти, Р – середина II -ой четверти. Ограничить значение переменной t для: (составить двойное неравенство) а) дуги МР; б) дуги РМ.
6. Записать двойное неравенство для выделенных участков графика:
Рис. 1
7.
Решите неравенства
, 
, 
, 
.
8. Преобразовать выражение .
На втором этапе обучения решению тригонометрических неравенств можно предложить следующие рекомендации, связанные с методикой организации деятельности учащихся. При этом нужно ориентироваться на уже имеющиеся у учащихся умения работать с тригонометрической окружностью или графиком, сформированные во время решения простейших тригонометрических уравнений.
Во-первых, мотивировать целесообразность получения общего приема решения простейших тригонометрических неравенств можно, обратившись, например, к неравенству вида
.
Используя знания и умения, приобретенные на подготовительном этапе, учащиеся приведут предложенное неравенство к виду
, но могут затрудниться в нахождении множества решений полученного неравенства, т.к. только лишь используя свойства функции синус решить его невозможно. Этого затруднения можно избежать, если обратиться к соответствующей иллюстрации (решение уравнения графически или с помощью единичной окружности).
Во-вторых, учитель должен обратить внимание учащихся на различные способы выполнения задания, дать соответствующий образец решения неравенства и графическим способом и с помощью тригонометрического круга.
Рассмотрим такие варианты решения неравенства
.
1. Решение неравенства с помощью единичной окружности.
На первом занятии по решению тригонометрических неравенств предложим учащимся подробный алгоритм решения, который в пошаговом представлении отражает все основные умения, необходимые для решения неравенства.
Шаг 1.
Начертим единичную окружность, отметим на оси ординат точку
и проведем через нее прямую, параллельную оси абсцисс. Эта прямая пересечет единичную окружность в двух точках. Каждая из этих точек изображает числа, синус которых равен
.
Шаг 2.
Эта прямая разделила окружность на две дуги. Выделим ту из них, на которой изображаются числа, имеющие синус больший, чем
. Естественно, эта дуга расположена выше проведенной прямой.
Рис. 2
Шаг 3.
Выберем один из концов отмеченной дуги. Запишем одно из чисел, которое изображается этой точкой единичной окружности
.
Шаг 4.
Для того чтобы выбрать число, соответствующее второму концу выделенной дуги, "пройдем" по этой дуге из названного конца к другому. При этом напомним, что при движении против часовой стрелки числа, которые мы будем проходить, увеличиваются (при движении в противоположном направлении числа уменьшались бы). Запишем число, которое изображается на единичной окружности вторым концом отмеченной дуги
.
Таким образом, мы видим, что неравенству
удовлетворяют числа, для которых справедливо неравенство
. Мы решили неравенство для чисел, расположенных на одном периоде функции синус. Поэтому все решения неравенства могут быть записаны в виде 
Учащимся нужно предложить внимательно рассмотреть рисунок и разобраться, почему все решения неравенства
могут быть записаны в виде
, 
.
Рис. 3
Необходимо обратить внимание учащихся на то, что при решении неравенств для функции косинус, прямую проводим параллельно оси ординат.
Графический способ решения неравенства.
Строим графики
и
, учитывая, что
.
Рис. 4
Затем записываем уравнение
и его решение
, 
, 
, найденное с помощью формул
, 
, 
.
(Придавая
n
значения 0, 1, 2, находим три корня составленного уравнения). Значения
являются тремя последовательными абсциссами точек пересечения графиков
и
. Очевидно, что всегда на интервале
выполняется неравенство
, а на интервале
– неравенство
. Нас интересует первый случай, и тогда добавив к концам этого промежутка число, кратное периоду синуса, получим решение неравенства
в виде:
, .
Рис. 5
Подведём итог. Чтобы решить неравенство
, надо составить соответствующее уравнение и решить его. Из полученной формулы найти корни
и
, и записать ответ неравенства в виде:
, .
В-третьих, факт о множестве корней соответствующего тригонометрического неравенства очень наглядно подтверждается при решении его графическим способом.
Рис. 6
Необходимо продемонстрировать учащимся, что виток, который является решением неравенства, повторяется через один и тот же промежуток, равный периоду тригонометрической функции. Так же можно рассмотреть аналогичную иллюстрацию для графика функции синус.
В-четвертых, целесообразно провести работу по актуализации у учащихся приемов преобразования суммы (разности) тригонометрических функций в произведение, обратить внимание школьников на роль этих приемов при решении тригонометрических неравенств.
Организовать такую работу можно через самостоятельное выполнение учащимися предложенных учителем заданий, среди которых выделим следующие:
В-пятых, от учащихся необходимо требовать обязательной иллюстрации решения каждого простейшего тригонометрического неравенства с помощью графика или тригонометрического круга. Обязательно следует обратить внимание на ее целесообразность, в особенности на применение круга, так как при решении тригонометрических неравенств соответствующая иллюстрация служит очень удобным средством фиксации множества решений данного неравенства
Знакомство учащихся с приемами решения тригонометрических неравенств, не являющихся простейшими, целесообразно осуществлять по следующей схеме: обращение к конкретному тригонометрическому неравенству обращение к соответствующему тригонометрическому уравнению совместный поиск (учитель – учащиеся) приема решения самостоятельный перенос найденного приема на другие неравенства этого же вида.
Чтобы систематизировать знания учащихся о тригонометрии, рекомендуем специально подобрать такие неравенства, решение которых требует различных преобразований, которые могут быть реализованы в процессе его решения, акцентировать внимание учащихся на их особенностях.
В качестве таких продуктивных неравенств можно предложить, например, следующие:
В заключение приведем пример комплекса задач по решению тригонометрических неравенств.
1. Решите неравенства:
2. Решите неравенства: 3. Найдите все решения неравенств: 4. Найдите все решения неравенств:а)
, удовлетворяющие условию 
;
б)
, удовлетворяющие условию 
.
5. Найдите все решения неравенств:
а) ;
б) ;
в) 
;
г) 
;
д) 
.
6. Решите неравенства:
а) ;
б) ;
в) ;
г) 
;
д) ;
е) ;
ж) 
.
7. Решите неравенства:
а)
;
б) ;
в) ;
г) .
8. Решите неравенства:
а) ;
б) ;
в) ;
г) 
;
д) 
;
е) ;
ж) 
;
з) .
Задания 6 и 7 целесообразно предложить ученикам, изучающим математику на повышенном уровне, задание 8 – учащимся классов с углубленным изучением математики.
§3. Специальные методы решения тригонометрических неравенств
Специальные методы решения тригонометрических уравнений – то есть те методы, которые можно использовать только для решения тригонометрических уравнений. Эти методы основаны на использовании свойств тригонометрических функций, а также на использовании различных тригонометрических формул и тождеств.
3.1. Метод секторов
Рассмотрим метод секторов для решения тригонометрических неравенств. Решение неравенств вида 
, где
P
(
x
)
и
Q
(
x
)
– рациональные тригонометрические функции (синусы, косинусы, тангенсы и котангенсы входят в них рационально), аналогично решению рациональных неравенств. Рациональные неравенства удобно решать методом интервалов на числовой оси. Его аналогом при решении рациональных тригонометрических неравенств является метод секторов в тригонометрическом круге, для
sinx
и
cosx
(
) или тригонометрическом полукруге для
tgx
и
ctgx
(
).
В методе интервалов каждому линейному множителю числителя и знаменателя вида 
на числовой оси соответствует точка 
, и при переходе через эту точку меняет знак. В методе секторов каждому множителю вида 
, где 
- одна из функций
sinx
или
cosx
и 
, в тригонометрическом круге соответствуют два угла 
и 
, которые делят круг на два сектора. При переходе через и функция меняет знак.
Необходимо помнить следующее:
а) Множители вида 
и 
, где 
, сохраняют знак для всех значений 
. Такие множители числителя и знаменателя отбрасывают, изменяя (если 
) при каждом таком отбрасывании знак неравенства на противоположный.
б) Множители вида 
и 
также отбрасываются. При этом, если это множители знаменателя, то в эквивалентную систему неравенств добавляются неравенства вида 
и 
. Если это множители числителя, то в эквивалентной системе ограничений им соответствуют неравенства и в случае строгого исходного неравенства, и равенства 
и 
в случае нестрогого исходного неравенства. При отбрасывании множителя 
или 
знак неравенства изменяется на противоположный.
Пример 1.
Решить неравенства: а) 
, б) 
.
имеем
функция, б) . Решить неравенство Имеем,
3.2. Метод концентрических окружностей
Данный метод является аналогом метода параллельных числовых осей при решении систем рациональных неравенств.
Рассмотрим пример системы неравенств.
Пример 5.
Решить систему простейших тригонометрических неравенств 
Сначала решим каждое неравенство отдельно (рисунок 5). В правом верхнем углу рисунка будем указывать для какого аргумента рассматривается тригонометрическая окружность.
Рис.5
Далее строим систему концентрических окружностей для аргумента х . Рисуем окружность и заштриховываем ее согласно решению первого неравенства, затем рисуем окружность большего радиуса и заштриховываем ее согласно решению второго, далее строим окружность для третьего неравенства и базовую окружность. Из центра системы через концы дуг проводим лучи так, чтобы они пересекали все окружности. На базовой окружности формируем решение (рисунок 6).
Рис.6
Ответ:
, 
.
Заключение
Все задачи курсового исследования были выполнены. Систематизирован теоретический материал: приведены основные типы тригонометрических неравенств и основные методы их решения (графический, алгебраический, метод интервалов, секторов и метод концентрических окружностей). К каждому методы был приведен пример решения неравенства. За теоретической частью следовала практическая. В ней составлен комплекс заданий по решению тригонометрических неравенств.
Данная курсовая может быть использована учащимися для самостоятельной работы. Школьники могут проконтролировать уровень усвоения данной темы, потренироваться в выполнении заданий различной сложности.
Проработав соответствующую литературу по данному вопросу, очевидно, можно сделать вывод о том, что умение и навыки решать тригонометрические неравенства в школьном курсе алгебры и начал анализа являются очень важными, развитие которых требует значительных усилий со стороны учителя математики.
Поэтому данная работа будет полезна учителям математики, так как дает возможность эффективно организовать подготовку учащихся по теме «Тригонометрические неравенства».
Исследование можно продолжить, расширив его до выпускной квалификационной работы .
Список использованной литературы
Богомолов, Н.В. Сборник задач по математике [Текст] / Н.В. Богомолов. – М.: Дрофа, 2009. – 206 с.
Выгодский, М.Я. Справочник по элементарной математике [Текст] / М.Я. Выгодский. – М.: Дрофа, 2006. – 509 с.
Журбенко, Л.Н. Математика в примерах и задачах [Текст] / Л.Н. Журбенко. – М.: Инфра-М, 2009. – 373 с.
Иванов, О.А. Элементарная математика для школьников, студентов и преподавателей [Текст] / О.А. Иванов. – М.: МЦНМО, 2009. – 384 с.
Карп, А.П. Задания по алгебре и началам анализа для организации итогового повторения и проведения аттестации в 11 классе [Текст] / А.П. Карп. – М.: Просвещение, 2005. – 79 с.
Куланин, Е.Д. 3000 конкурсных задач по математике [Текст] / Е.Д. Куланин. – М.: Айрис-пресс, 2007. – 624 с.
Лейбсон, К.Л. Сборник практических заданий по математике [Текст] / К.Л. Лейбсон. – М.: Дрофа, 2010. – 182 с.
Локоть, В.В. Задачи с параметрами и их решение. Тригонометрия: уравнения, неравенства, системы. 10 класс [Текст] / В.В. Локоть. – М.: АРКТИ, 2008. – 64 с.
Манова, А.Н. Математика. Экспресс-репетитор для подготовки к ЕГЭ: уч. пособие [Текст] / А.Н. Манова. – Ростов-на-Дону: Феникс, 2012. – 541 с.
Мордкович, А.Г. Алгебра и начала математического анализа. 10-11 классы. Учебник для учащихся общеобразовательных учреждений [Текст] / А.Г. Мордкович. – М.: Айрис-пресс, 2009. – 201 с.
Новиков, А.И. Тригонометрические функции, уравнения и неравенства [Текст] / А.И. Новиков. – М.: ФИЗМАТЛИТ, 2010. – 260 с.
Оганесян, В.А. Методика преподавания математики в средней школе: Общая методика. Учеб. пособие для студентов физ. - мат. фак. пед. ин-тов. [Текст] / В.А. Оганесян. – М.: Просвещение, 2006. – 368 с.
Олехник, С.Н. Уравнения и неравенства. Нестандартные методы решения [Текст] / С.Н. Олехник. – М.: Изд-во Факториал, 1997. – 219 с.
Севрюков, П.Ф. Тригонометрические, показательные и логарифмические уравнения и неравенства [Текст] / П.Ф. Севрюков. – М.: Народное образование, 2008. – 352 с.
Сергеев, И.Н. ЕГЭ: 1000 задач с ответами и решениями по математике. Все задания группы С [Текст] / И.Н. Сергеев. – М.: Экзамен, 2012. – 301 с.
Соболев, А.Б. Элементарная математика [Текст] / А.Б. Соболев. – Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. – 81 с.
Фенько, Л.М. Метод интервалов в решении неравенств и исследовании функций [Текст] / Л.М. Фенько. – М.: Дрофа, 2005. – 124 с.
Фридман, Л.М. Теоретические основы методики обучения математике [Текст] / Л.М. Фридман. – М.: Книжный дом «ЛИБРОКОМ», 2009. – 248 с.
Приложение 1
Графическая интерпретация решений простейших неравенств
Рис. 1
Рис. 2
Рис.3
Рис.4
Рис.5
Рис.6
Рис.7
Рис.8
Приложение 2
Решения простейших неравенств
ОПРЕДЕЛЕНИЕ
Тригонометрическими неравенствами называются неравенства, которые содержат переменную под знаком тригонометрической функции.
Решение тригонометрических неравенств
Решение тригонометрических неравенств зачастую сводится к решению простейших тригонометрических неравенств вида: \(\ \sin x a \), \(\ \cos x > a \), \(\ \operatorname{tg} x > a \), \(\ \operatorname{ctg} x > a \), \(\ \sin x \leq a \), \(\ \cos x \leq a \), \(\ \operatorname{tg} x \leq a \), \(\ \operatorname{ctg} x \leq a \), \(\ \sin x \geq a \), \(\ \cos \geq a \), \(\ \operatorname{tg} x \geq a \), \(\ \operatorname{tg} x \geq a \)
Решаются простейшие тригонометрические неравенства графически или с помощью единичной тригонометрической окружности.
По определению, синусом угла \(\ \alpha \) есть ординатой точки \(\ P_{\alpha}(x, y) \) единичного круга (рис. 1), а косинусом – абсцисса этой точки. Этот факт используется при решении простейших тригонометрических неравенств с косинусом и синусом с помощью единичного круга.
Примеры решения тригонометрических неравенств
Решить неравенство \(\ \sin x \leq \frac{\sqrt{3}}{2} \)
Поскольку \(\ \left|\frac{\sqrt{3}}{2}\right| , то это неравенство имеет решение и его можно решить двумя способами
Первый способ. Решим это неравенство графически. Для этого построим в одной системе координат график синуса \(\ y=\sin x \) (рис. 2) и прямой \(\ y=\frac{\sqrt{3}}{2} \)
Выделим промежутки, на которых синусоида расположена ниже графика прямой \(\ y=\frac{\sqrt{3}}{2} \) . Найдем абсциссы \(\ x_{1} \) и \(\ x_{2} \) точек пересечения этих графиков: \(\ x_{1}=\pi-\arcsin \frac{\sqrt{3}}{2}=\pi-\frac{\pi}{3}=\frac{2 \pi}{3} x_{2}=\arcsin \frac{\sqrt{3}}{2}+2 \pi=\frac{\pi}{3}+2 \pi=\frac{7 \pi}{3} \)
Получили интервал \(\ \left[-\frac{4 \pi}{3} ; \frac{\pi}{3}\right] \) но так как функцию \(\ y=\sin x \) периодическая и имеет период \(\ 2 \pi \) , то ответом будет объединение интервалов: \(\ \left[\frac{2 \pi}{3}+2 \pi k ; \frac{7 \pi}{3}+2 \pi k\right] \), \(\ k \in Z \)
Второй способ. Построим единичную окружность и прямую \(\ y=\frac{\sqrt{3}}{2} \) , точки их пересечения обозначим \(\ P_{x_{1}} \) и \(\ P_{x_{2}} \) (рис. 3). Решением исходного неравенства будет множество точек ординаты, которых меньше \(\ \frac{\sqrt{3}}{2} \) . Найдем значение \(\ \boldsymbol{I}_{1} \) и \(\ \boldsymbol{I}_{2} \) , совершая обход против часовой стрелки, \(\ x_{1} Рис. 3
\(\ x_{1}=\pi-\arcsin \frac{\sqrt{3}}{2}=\pi-\frac{\pi}{3}=\frac{2 \pi}{3} x_{2}=\arcsin \frac{\sqrt{3}}{2}+2 \pi=\frac{\pi}{3}+2 \pi=\frac{7 \pi}{3} \)
Учитывая периодичность функции синус, окончательно получим интервалы \(\ \left[\frac{2 \pi}{3}+2 \pi k ; \frac{7 \pi}{3}+2 \pi\right] \), \(\ k \in Z \)
Решить неравенство \(\ \sin x>2 \)
Синус – функция ограниченная: \(\ |\sin x| \leq 1 \) , а правая часть данного неравенства больше единицы, поэтому решений нет.
Решить неравенство \(\ \cos x>\frac{1}{2} \)
Данное неравенство можно решить двумя способами: графически и с помощью единичного круга. Рассмотрим каждый из способов.
Первый способ. Изобразим в одной системе координат функции, описывающие левую и правую части неравенства, то есть \(\ y=\cos x \) и \(\ y=\frac{1}{2} \) . Выделим промежутки, на которых график функции косинус \(\ y=\cos x \) расположен выше графика прямой \(\ y=\frac{1}{2} \) (рис. 4).
Найдем абсциссы точек \(\ \boldsymbol{x}_{1} \) и \(\ x_{2} \) – точек пересечения графиков функций \(\ y=\cos x \) и \(\ y=\frac{1}{2} \) , которые являются концами одного из промежутков, на котором выполняется указанное неравенство. \(\ x_{1}=-\arccos \frac{1}{2}=-\frac{\pi}{3} \); \(\ x_{1}=\arccos \frac{1}{2}=\frac{\pi}{3} \)
Учитывая, что косинус – функция периодическая, с периодом \(\ 2 \pi \) , ответом будет значения \(\ x \) из промежутков \(\ \left(-\frac{\pi}{3}+2 \pi k ; \frac{\pi}{3}+2 \pi k\right) \), \(\ k \in Z \)
Второй способ. Построим единичную окружность и прямую \(\ x=\frac{1}{2} \) (так как на единичной окружности косинусам отвечает ось абсцисс). Обозначим \(\ P_{x_{1}} \) и \(\ P_{x_{2}} \) (рис. 5) – точки пересечения прямой и единичной окружности. Решением исходного уравнения будет множество точек абсциссы, которых меньше \(\ \frac{1}{2} \) . Найдем значение \(\ x_{1} \) и \(\ 2 \) , совершая обход против часовой стрелки так, чтобы \(\ x_{1} Учитывая периодичность косинуса, окончательно получим интервалы \(\ \left(-\frac{\pi}{3}+2 \pi k ; \frac{\pi}{3}+2 \pi k\right) \),\(\ k \in Z \)
Решить неравенство \(\ \operatorname{ctg} x \leq-\frac{\sqrt{3}}{3} \)
Построим в одной системе координат графики функций \(\ y=\operatorname{ctg} x \), \(\ y=-\frac{\sqrt{3}}{3} \)
Выделим промежутки, на которых график функции \(\ y=\operatorname{ctg} x \) расположен не выше графика прямой \(\ y=-\frac{\sqrt{3}}{3} \) (рис. 6).
Найдем абсциссу точки \(\ x_{0} \) , которая является концом одного из промежутков, на котором неравенство \(\ x_{0}=\operatorname{arcctg}\left(-\frac{\sqrt{3}}{3}\right)=\pi-\operatorname{arcctg}\left(\frac{\sqrt{3}}{3}\right)=\pi-\frac{\pi}{3}=\frac{2 \pi}{3} \)
Другим концом этого промежутка есть точка \(\ \pi \) , а функция \(\ y=\operatorname{ctg} x \) в этой точке неопределенна. Таким образом, одним из решением данного неравенства является промежуток \(\ \frac{2 \pi}{3} \leq x
Тригонометрические неравенства со сложным аргументом
Тригонометрические неравенства со сложным аргументом можно свести к простейшим тригонометрическим неравенствам с помощью замены. После его решения делается обратная замена и выражается исходная неизвестная.
Решить неравенство \(\ 2 \cos \left(2 x+100^{\circ}\right) \leq-1 \)
Выразим в правой части данного неравенства косинус: \(\ \cos \left(2 x+100^{\circ}\right) \leq-\frac{1}{2} \)
Ведем замену \(\ t=2 x+100^{\circ} \) , после чего данное неравенство преобразуется к простейшему неравенству \(\ \cos t \leq-\frac{1}{2} \)
Решим его, используя единичную окружность. Построим единичный круг и прямую \(\ x=-\frac{1}{2} \) . Обозначим \(\ P_{1} \) и \(\ P_{2} \) – точки пересечения прямой и единичной окружности (рис. 7).
Решением исходного неравенства будет множество точек абсциссы, которых не больше \(\ -\frac{1}{2} \). Точке \(\ P_{1} \) соответствует угол \(\ 120^{\circ} \) , а точке \(\ P_{2} \) . Таким образом, учитывая период косинуса, получим \(\ 120^{\circ}+360^{\circ} \cdot n \leq t \leq 240^{\circ}+360^{\circ} \cdot n \), \(\ n \in Z \)
Сделаем обратную замену \(\ t=2 x+100^{\circ} 120^{\circ}+360^{\circ} \cdot n \leq 2 x+100^{\circ} \leq 240^{\circ}+360^{\circ} \cdot n \), \(\ n \in Z \)
Выразим \(\ \mathbf{x} \), для сначала этого из каждой части неравенства вычтем \(\ 100^{\circ} 120^{\circ}-100^{\circ}+360^{\circ} \cdot n \leq 2 x+100^{\circ}-100^{\circ} \leq 240^{\circ}-100^{\circ}+360^{\circ} \cdot n \), \(\ n \in Z \); \(\ 20^{\circ}+360^{\circ} \cdot n \leq 2 x \leq 140^{\circ}+360^{\circ} \cdot n \), \(\ n \in Z \)
а затем, разделим на 2 \(\ \frac{20^{\circ}+360^{\circ} \cdot n}{2} \leq \frac{2 x}{2} \leq \frac{140^{\circ}+360^{\circ} \cdot n}{2} \), \(\ n \in Z \); \(\ 10^{\circ}+180^{\circ} \cdot n \leq x \leq 70^{\circ}+180^{\circ} \cdot n \), \(\ n \in Z \)
Двойные тригонометрические неравенства
Решить двойное тригонометрическое неравенство \(\ \frac{1}{2}
Введем замену \(\ t=\frac{x}{2} \) , тогда исходное неравенство примет вид \(\ \frac{1}{2}
Решим его, используя единичную окружность. Так как на единичной окружности синусу соответствует ось ординат, выделим на ней множество ординаты которых больше \(\ x=\frac{1}{2} \) и меньше или равно \(\ \frac{\sqrt{2}}{2} \) . На рисунке 8 эти точки будут расположены на дугах \(\ P_{t_{1}} \), \(\ P_{t_{2}} \) и \(\ P_{t_{3}} \), \(\ P_{t_{4}} \) . Найдем значение \(\ t_{1} \), \(\ t_{2} \), \(\ t_{3} \), \(\ t_{4} \) , совершая обход против часовой стрелки, причем \(\ t_{1} \(\ t_{3}=\pi-\arcsin \frac{\sqrt{2}}{2}=\pi-\frac{\pi}{4}=\frac{3 \pi}{4} \); \(\ t_{4}=\pi-\arcsin \frac{1}{2}=\pi-\frac{\pi}{6}=\frac{5 \pi}{6} \)
Таким образом, получаем два интервала, которые, учитывая периодичность функции синус, можно записать следующим образом \(\ \frac{\pi}{6}+2 \pi k \leq t \frac{\pi}{4}+2 \pi k \quad \frac{3 \pi}{4}+2 \pi k Сделаем обратную замену \(\ t=\frac{x}{2} \frac{\pi}{6}+2 \pi k \leq \frac{x}{2} \frac{\pi}{4}+2 \pi k \), \(\ \frac{3 \pi}{4}+2 \pi kВыразим \(\ \mathbf{x} \), для этого умножим все стороны обои неравенств на 2, получим \(\ \frac{\pi}{3}+4 \pi k \leq x
Решение простейших тригонометрических уравнений
Для начала вспомним формулы для решения простейших тригонометрических уравнений .
- $sinx=a$
- $cosx=a$
- $tgx=a$
- $ctgx=a$
Решение простейших тригонометрических неравенств.
Для решения простейших тригонометрических неравенств нам вначале необходимо решить соответствующее уравнение, а затем, используя тригонометрическую окружность , найти решение неравенства . Рассмотрим решения простейших тригонометрических неравенств на примерах.
Пример 1
$sinx\ge \frac{1}{2}$
Найдем решение тригонометрического неравенства $sinx=\frac{1}{2}$
\ \
Рисунок 1. Решение неравенства $sinx\ge \frac{1}{2}$.
Так как неравенство имеет знак «больше или равно», то решение лежит на верхней дуге окружности (относительно решения уравнения).
Ответ: $\left[\frac{\pi }{6}+2\pi n,\frac{5\pi }{6}+2\pi n\right]$.
Пример 2
Найдем решение тригонометрического неравенства $cosx=\frac{\sqrt{3}}{2}$
\ \
Отметим решение на тригонометрической окружности
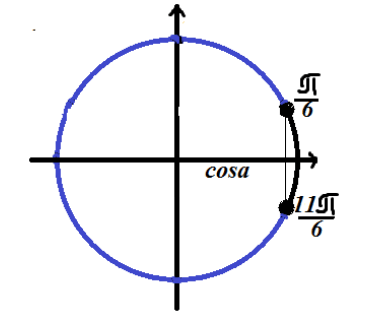
Так как неравенство имеет знак «меньше», то решение лежит на дуге окружности, расположенной слева (относительно решения уравнения).
Ответ: $\left(\frac{\pi }{6}+2\pi n,\frac{11\pi }{6}+2\pi n\right)$.
Пример 3
$tgx\le \frac{\sqrt{3}}{3}$
Найдем решение тригонометрического неравенства $tgx=\frac{\sqrt{3}}{3}$
\ \
Здесь также нам понадобится область определения. Как мы помним у функции тангенса $x\ne \frac{\pi }{2}+\pi n,n\in Z$
Отметим решение на тригонометрической окружности
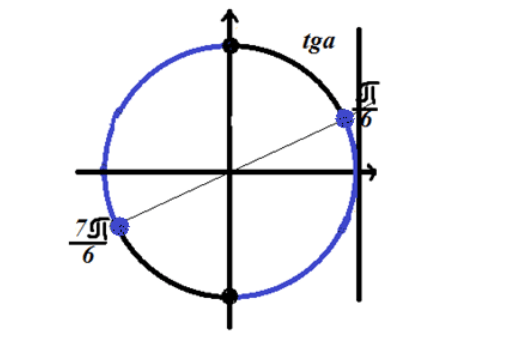
Рисунок 3. Решение неравенства $tgx\le \frac{\sqrt{3}}{3}$.
Так как неравенство имеет знак «меньше или равно», то решение лежит на дугах окружности, отмеченных синим на рисунке 3.
Ответ:$\ \left(-\frac{\pi }{2}+2\pi n\right.,\left.\frac{\pi }{6}+2\pi n\right]\cup \left(\frac{\pi }{2}+2\pi n,\right.\left.\frac{7\pi }{6}+2\pi n\right]$
Пример 4
Найдем решение тригонометрического неравенства $ctgx=\sqrt{3}$
\ \
Здесь также нам понадобится область определения. Как мы помним у функции тангенса $x\ne \pi n,n\in Z$
Отметим решение на тригонометрической окружности
Рисунок 4. Решение неравенства $ctgx\le \sqrt{3}$.
Так как неравенство имеет знак «больше», то решение лежит на дугах окружности, отмеченных синим на рисунке 4.
Ответ:$\ \left(2\pi n,\frac{\pi }{6}+2\pi n\right)\cup \left(\pi +2\pi n,\frac{7\pi }{6}+2\pi n\right)$
Проект по алгебре «Решение тригонометрических неравенств» Выполнила ученица 10 «Б» класса Казачкова Юлия Руководитель: учитель математики Кочакова Н.Н.
Цель Закрепить материал по теме «Решение тригонометрических неравенств» и создать памятку ученикам для подготовки к предстоящему экзамену.
Задачи Обобщить материал по данной теме. Систематизировать полученную информацию. Рассмотреть данную тему в ЕГЭ.
Актуальность Актуальность выбранной мною темы заключается в том, что задания на тему «Решение тригонометрических неравенств» входят в задания ЕГЭ.
Тригонометрические неравенства Неравенство - это отношение, связывающее два числа или выражения посредством одного из знаков: (больше); ≥ (больше или равно). Тригонометрическое неравенство – это неравенство, содержащее тригонометрические функции.
Тригонометрические неравенства Решение неравенств, содержащих тригонометрические функции, сводится, как правило, к решению простейших неравенств вида: sin x>a, sin xa, cos x a, tg x a, ctg x
Алгоритм решения тригонометрических неравенств На оси, соответствующей заданной тригонометрической функции, отметить данное числовое значение этой функции. Провести через отмеченную точку прямую, пересекающую единичную окружность. Выделить точки пересечения прямой и окружности с учетом строгого или нестрогого знака неравенства. Выделить дугу окружности, на которой расположены решения неравенства. Определить значения углов в начальной и конечной точках дуги окружности. Записать решение неравенства с учетом периодичности заданной тригонометрической функции.
Формулы решения тригонометрических неравенств sinx >a; x (arcsin a + 2πn; π- arcsin a + 2πn). sinx a; x (- arccos a + 2πn; arccos a + 2πn). cosx a; x (arctg a + πn ; + πn). tgx a; x (πn ; arctg + πn). ctgx
Графическое решение основных тригонометрическх неравенств sinx >a
Графическое решение основных тригонометрическх неравенств sinx Графическое решение основных тригонометрическх неравенств cosx >a Графическое решение основных тригонометрическх неравенств cosx Графическое решение основных тригонометрическх неравенств tgx >a Графическое решение основных тригонометрическх неравенств tgx Графическое решение основных тригонометрическх неравенств ctgx >a